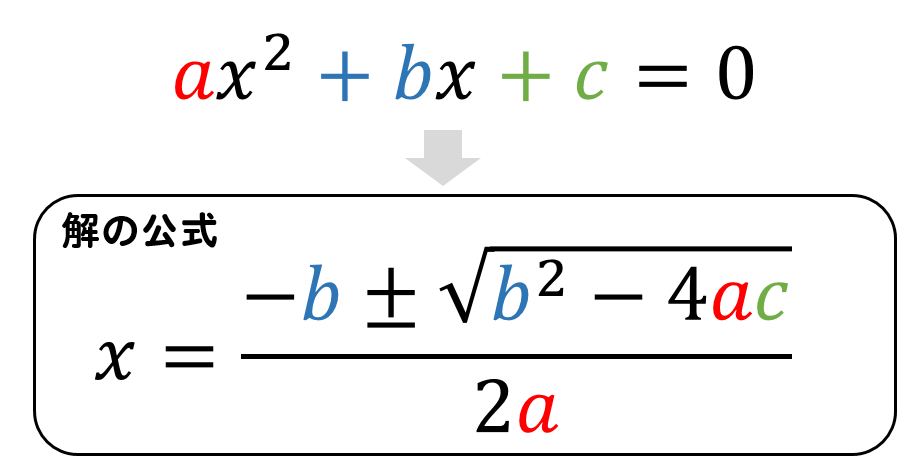部位 と 流れる 血液 と の 組み合わせ方程式の有理数解 | 高校数学の美しい物語. 方程式の有理数解を見つける方法を解説します。 目次. 高次方程式と有理数解. 有理数解の見つけ方. 有理数解に関する補足. 定理の証明. 高次方程式と有理数解. x^3-x^2-x-2=0 x3 − x2 −x −2 = 0. のような「整数係数多項式 =0 = 0 」という方程式を考えます。 左辺を f (x) f (x) と置きます。 高次方程式の解き方. fleft (alpharight)=0 f (α) = 0 を満たす有理数. alpha α を 頑張って見つける 。 左辺を. left (x-alpharight) (x −α) で割る. 二次方程式になるまで上記を繰り返す。 二次方程式は解の公式か因数分解で解ける。 例1. 有理数解とは?有理数解を持つ・持たないが関わる定理や入試 . 有理数解とは、方程式の解のうち、2つの整数の分数の形で表せるようなもののことです。 入試問題ではしばしば、「この方程式が有理数解を持つような条件を求めよ」というような形式の問題が出題されることがあります。. 2次方程式の解が有理数となる条件 - 数学カフェjr. 【問題】 xについての 2次方程式. 2x2 + (4c − 3)x + 2c2 − c − 11 = 0. の解が異なる2つの 有理数 となるとき、 自然数 cは何通り考えられるか? 初見の人は、とりあえず解いてみましょう。 あまり言うとネタバレになってしまいますが、うっかりミスをしてしまう人が少なからずいそうな問題です。 なお、中学生も. 「 有理数 」 という言葉は一応習っているはずですが、 「実数という数の世界で 無理数 ではない数」 ということだけ理解していれば、本問題は解けますね。 (※整数問題でよく用いられる"定義"まで理解している必要はありませんね。 【解説】 " 2次方程式 の解の判別式" とは、その解において. "√の中の数を表す式" のことでしたね。. 整数係数方程式の整数解・有理数解に関する定理の証明 - 受験の月. $整数係数n次方程式 a_nx^n+a_{n-1}x^{n-1}+・・・+a_1x+a_0=0 (a_0, a_n≠0)がある.$ $この方程式が有理数解をもつとき, その解は a_0,の約数}{a_n,の約数} の形であることを証明せよ.$ 本項の中で最も重要な定理である. 証明を理解. 整数係数のn次方程式の有理数解 | 数学の庭. 整数係数のn次方程式の有理数解. 関数・方程式と不等式. 【定理】. 整数係数のn次方程式. anxn + an − 1xn − 1 + ⋯ + a1x + a0 = 0(a0, a1, ⋯, an は整数) が有理数解を持つならば,その解は. a0の約数 anの約数 に限られる。. とくに an = ± 1 のとき, 有理数解は . 【頻出】有理数の解をもつ⇒その解は整数|2001神戸大学・理 . 解答. (1) 3 次方程式 x3 + ax2 + bx + c = 0 が有理数の解をもつとき、 x = n m ( m と n は互いに素な整数 ) とおける.これを 3 次方程式に代入すると、 ( n m)3 + a( n m)2 + b ⋅ n m + c = 0. m3 を両辺にかけて整理すると、 n3 + amn2 + bm2n + cm3 = 0. n3 = −m(an2 + bmn + cm2) m と n は互いに素な整数であるから、 m = ±1. したがって、 x = n m = ±n. となり整数解となる.以上より題意は示された.. うち の 子 は adhd ブログ
twitter 晒 され た 対処(2) 方程式 x3 + 2x2 + 2 = 0 が、有理数の解をもつと仮定する.. (1)の結果より、その解は整数解となる.. 高次方程式の有理数解|オンライン予備校 e-YOBI ネット塾. 高次方程式の有理数解. 証明. 問題. まとめ. 高次方程式の有理数解. 波 板 重ね しろ 縦
相場 と は おみくじ3次方程式などを解くときに暗黙に成立するとしていた、次の定理について考えてみましょう。 有理解の定理. n n 次方程式. 爪 挟ん だ 内出血
歯 の 神経 抜い た 後 痛みa0xn +a1xn−1 + a2xn−2 + ⋯+ an−1x +an = 0 a 0 x n + a 1 x n − 1 + a 2 x n − 2 + ⋯ + a n − 1 x + a n = 0. ( a0,a1,…,an a 0, a 1, …, a n は整数) が有理数の解をもつとき、その有理数解は anの約数 a0の約数 a n の 約 数 a 0 の 約 数 とかける。 普段つかっている定理ですよね? 3次方程式を解くときに因数定理を使って… あ…. 有理数解の定理 - okke. 概要. 因数分解などにすごく役に立つ 「有理数解の定理」 をマスターしよう。 証明にも整数問題の考え方が詰まっているので、合わせておさえておこう。 まず内容は、 整数係数の 次方程式. を考えたとき、この方程式の有理数解は、 の 約 数 の 約 数. の形で必ず表される (負の約数も考える) 。 ただし、ここで考えているのは 次方程式なので 。 また とすると、上の方程式を でくくることで、 と、 次方程式. に分解されるので、ここでは とする。 大事なのは、 有理数解を持つとすると、その可能性はだいぶ絞られる ということで、上で表される が全て解になるわけではないし、必ず有理数解が存在するということではない点に注意しよう!. 方程式の有理数解の良問解説動画!解説ノート付き! - okke. 2021年5月29日. ぶおとこばってん. ばってんです♨️. 今日は、 方程式の有理数解の定番の良問 について、深く掘り下げて解説します。 問題はこちらです、まずは是非自力でチャレンジしてみましょう! (数学1A2B良問演習シリーズ100選、第15問目です) 余りによる分類がポイントです! (ここでは偶数・奇数に注目) それでは、こちらの動画で解説や答えを確認しましょう! 整数問題の考え方のポイントや、答案を書く上での論理の流れ についても掘り下げて解説しているので、特に独学の方々にオススメです。 良問演習100選の他の問題 はこちらから確認! 解説ノートも下からダウンロード できます! この記事の補足資料. 二次方程式の有理数解の解説ノート(高校数学良問演習1A2B No.15). PDF 1章 はじめに - 学校法人学習院. 次方程式の解の公式を学び,整数や有理数でない数,すなわち無理数を導入. し,さらに高校では,すべての. 2. 次方程式が解をもつように,数の範囲を複素数にまで広. げていった.この講義では,素朴な立場に戻り,方程式の解の範囲を整数や有理数に限. 定して,解の存在やその解き方に着目してみよう. たとえば, 3. 次方程式. x3 3x2. 大間 の マグロ 通販
眼科 疾患 と は+. 5x. 6 = 0. を解くことを考える.高校の【数学. II. ろく さん 亭 フリーズ ドライ
華氏 100 度 は 摂氏 何 度】では,解の候補として,定数項の約数. 高次方程式の有理数解 - YouTube. 高次方程式の有理数解. 鈴木貫太郎. 150K subscribers. Subscribe. 109. 7.3K views 2 years ago. 過去動画の大学別・分野別検索はHPから antaro1966.com この1冊で高校数学の基本の90%が身につく「中学の知識でオイラーの公式がわかる」 mzn.to/2t28U8C Show. コツ | 高校数学の美しい物語. isolated fudging: f (a, b, c)+f (b, c, a)+f (c, a, b)geq k f (a,b,c)+ f (b,c,a)+f (c,a,b) ≥ k. を証明する代わりに. f (a, b, c)geq dfrac {ka^r} {a^r+b^r+c^r} f (a,b,c) ≥ ar +br +crkar. を証明する手法. → isolated fudging. 方程式の有理数解. 指数方程式と有理数解 | 教えて数学理科. 指数方程式と有理数解 | 教えて数学理科. 2022.04.27. 指数方程式の有理数解に関する問題について見ていきます。 (例題) (1) 2r = 3 を満たす r は有理数でないことを示せ。 (2) 2x3−2y = 3x2y−6 を満たす有理数 x, y を求めよ。 (解答) (1) 3-√ が無理数であることの証明の場合と同様に、 r = n m (有理数)と仮定して、矛盾を導きます。 (背理法) 3 > 1 より、 r は正の数。 ここで与式を満たす r は有理数であると仮定すると、 r = n m ( m, n は互いに素な 正 の 整数) とおける。 与式より. 等々力 渓谷 駐輪場
会津 の 女性2 n m = 3. 両辺 m 乗して. 2m = 3n ・・・①. 有理数係数のn次方程式の無理数解 | 数学の庭. 有理数係数のn次方程式の無理数解. 関数・方程式と不等式. 有理数係数のn次方程式の無理数解. 
p, q, r p, q, r を有理数, r√ r を無理数, q ≠ 0 q ≠ 0 とする。 有理数係数の n n 次方程式. anxn + an−1xn−1 + ⋯ + a1x +a0 = 0 a n x n + a n − 1 x n − 1 + ⋯ + a 1 x + a 0 = 0. が p + q r√ p + q r を解にもてば, p − q r√ p − q r もまた解である。 目次. 証明. 例題. 証明. 3次方程式の有理数解の記述【深掘り高校数学】 - YouTube. 方程式の有理数解について、記述の書き方を深く検討するピンポイント動画です。有理数解の置き方をいつも迷ってしまう方にオススメです!清 . 整数係数多項式の有理数解|思考力を鍛える数学 - 思考力を . 有理数解. 文字通り,有理数であるような解を有理数解とよびます.. たとえば,方程式 $ (x-2) (x-sqrt {3}) (x+sqrt {3})=0$ の解は $$x=2,pm sqrt {3}$$ の $3$ つですが,このうち,有理数解は $2$ のみです.. また,方程式 $x^2-2x-1=0$ の解は $$x=1pm sqrt {5}$$ の $2$ つなので,有理数解はありません.このように,有理数解が存在しない方程式も当然存在します.. 定理の主張. 係数がすべて整数であるような多項式について,最高次の係数と定数項から,有理数解の候補を絞ることができる.. というのが定理の主張です.証明は次節で行うとして,具体例を見てみましょう.. ・$x^3-3x-2$. PDF 坂内健一 - 慶應義塾大学理工学部数理科学科. Birch and Swinnerton-Dyer予想(BSD予想)について解説し、方程式の有 理数解を求める問題に幾何がどう関わってくるか、紹介します。 1. Diophantine問題と幾何 方程式が与えられたとき、その方程式の整数解や有理数解を求める問題は、 Diophantine問題と呼ばれています。 Example 1.1. 例えばx2+ y2= 1という方程式が与えられたとき、この 場合のDiophantine問題は、この方程式をみたすx;y 2 Zやx;y 2 Qがど れだけあるか調べるという問題です。 ちなみにこの場合、整数解は、(x;y) = ( 1;0);(0; 1)です。 有理数解がどれだけあるか、分かりますでしょうか? Example 1.2. 整数係数n次方程式の有理数解[今週の定理・公式No.7] - YouTube. 整数係数n次方程式の有理数解[今週の定理・公式No.7]. Masaki Koga [数学解説] 70.7K subscribers. Subscribed. 345. 11K views 4 years ago 今週の定理・公式. 今週の定理公式シリーズは,毎週金曜日夜18:30投稿.. 公式や定理の証明をおさらいしよう,証明を理解すればさらに広がった視野が持てるよう .more. 有理根定理 - Wikipedia. 有理根定理 (ゆうりこんていり、 英: rational root theorem )は 整数 係数の 代数方程式. の 有理数 の解に対する制約を述べた定理である。 有理根定理は次のような言明である: 定数項 a0 および最高次の係数 an がゼロでないなら、有理数解 x = p/q を 互いに素 ( 最大公約数 が 1 )な整数 p, q で表したとき、 p, q は以下の条件を満たす。 p は a0 の 約数. q は an の約数. 有理根定理は、 多項式 の 因数分解 に関する ガウスの補題 ( 英語版 ) の特別な場合に当たる。 また、最高次の係数 an が 1 であるとき成り立つ 整数根定理 (integral root theorem) は、有理根定理の特別な場合である。. 
方程式計算機 - Symbolab. 無料の方程式計算機 - すべてのステップで,線形,二次,多項式,根号方程式,指数および対数方程式を解きます。. 方程式を入力して,解,ステップ,およびグラフを取得します. PDF Euclid 3 - 立命館大学. この節では, 有理数係数をもつ3次方程式と作図可能数との関係 について述べる. 有理係数からなる3次方程式x3 +ax2 +bx+c = 0が有理数根 を一つ持つとすると, x3 +ax2 +bx+c = (x )(x2 +px+q) = 0 p = +a, q = 2 +a +b)と変形でき, 2次x2 +. 【簡単】二次方程式の解の公式と、判別式について優しく解説 . 中学3年生で習う公式の1つに二次方程式の解の公式があります。 とても複雑な公式のため、覚えられない、理解できないと苦労している方も多いのではないでしょうか。 本記事では、解の公式の導出の仕方と判別式との関係性について優しく解説していきます。. 三次方程式の解き方3パターンと例題5問 | 高校数学の美しい物語. 解答. 公式 (B)を使って左辺を因数分解すると, (x-2)^3=0 (x− 2)3 = 0. よって,答えは x=2 x = 2 のみ(三重解) 三次方程式の解き方2(因数定理) 次は2つめのパターンです。 因数定理を使って,三次方程式 ax^3+bx^2+cx+d=0 ax3 +bx2 +cx+d = 0 を解きましょう。 解き方の流れ. 方程式を満たす有理数. alpha α を頑張って1つ探す. 左辺を. 令和6年度(2024年)大阪府高校入試問題数学の解説c問題も . 
令和6年度(2024年度)大阪府の高等学校入学者選抜学力検査テスト、数学の問題を解説します!難易度の高いC問題も分かりやすく解説てますよー! それではどーぞ!数学の先生どこよりも分かりやすく解説しているよ! A問題 1,21(1)正負の数の加法、減法(2)正負の数の乗法、除法(3 . やさしい理系数学~1~|【技術士】行政書士ささきしんや事務所. かつ だから、 で、 なので、 が言える。. サラリーマン兼業の行政書士、佐々木信也です。. 当事務所は、あまり行政書士の業務を行っておりません。. 当職は、普段は会社に勤めております。. 資格試験の勉強で作成した回答案を中心に掲載してまいります . 中学数学「中3数学の単元別テスト一覧」 | Pikuu|中学生の . ・平方根では、その概念と有理数、無理数の概念を組み合わた問題や平方根そのものの計算を学びます。 ・二次方程式、平方根の性質、因数分解の性質を利用して解く問題や解の公式を利用して解く方法を学びます。 ・二次関数では . 高校数学の整数問題です。 -不定方程式 7x + 6y = n が 6 個 . 3x-5y=6の1時不定方程式の整数解を求めよ 上が問題集の回答です。 私の下 2 2023/02/26 11:57 大学・短大 問題の解説でわからないところがあるのですが、 • 各位の数がそれぞれ異なる3桁の自然数のうち、各位の 3 2024/01/11 19:21. 【線形代数】連立方程式 #線形代数 - Qiita. 未知数の数>式の数 これが成り立つと解が複数あることになる 掃き出し法によって単位行列にする方法があるが解が複数ある場合は単位行列にならない 零ベクトルになるケースも解が複数ある場合に起こる. 掃き出し法により3行目の解が零行列になって . 「解の公式」は、テキトーに作られているわけじゃないんです . いいねの数:70スタディサプリ公式 (@studysapuri_official)のTikTok (ティックトック) 動画:「「解の公式」は、テキトーに作られているわけじゃないんです!! #解の公式 #数学 #二次方程式 #二次方程式の解の公式で苦戦中」。. オリジナル楽曲 - スタディサプリ公式。. a,bを有理数とする。2次方程式x²+ax+b=0の1つの解が1+√. - Yahoo!知恵袋. x²+ax+b=0の2解をα,βとする。 α+β=-a αβ=b が成り立ちます。 1つの解が1+√2なので、 もう1つの解はその共役数1-√2でありますので この2解をα,βに代入したら求まります。. 微分方程式の解法(同次形・線形微分方程式) | 高校数学の美しい物語. 様々な種類がある微分方程式のうち,同次形の微分方程式と(1階・2解の)線形微分方程式の一般解を求める解法を紹介します。その学ぶ意味が明確に理解できるように,線形微分方程式は物理で登場する単振動を例に挙げて説明を行います。. 二次方程式の解の公式 - Wikipedia. 概要. 二次方程式. の解は. 二次方程式の解の公式の導出には 平方完成 が行われるが、他の方法として、 因数分解 などがある。. 逆に、因数分解が困難な二次式は、二次方程式の解の公式から 因数定理 により因数分解することができる。. 歴史的には、二次 . 3分でわかる!解の公式をつかった二次方程式の解き方 | Qikeru:学びを楽しくわかりやすく. っていう二次方程式の解xは、 x = {-b±√(b² - 4ac)}/2a. になるんだよ。 これね。 ノートにでっかく書いて、見えるとこに貼っとこう。 長い付き合いになるからさ。 高校へ行っても、解の公式はついてくるんだ。 解の公式はどんなときに使うのー?. 【微分方程式】よくわかる 2階/同次/線形 の一般解と基本例題 | ばたぱら. ここでは、特性方程式を用いた 2階同次線形微分方程式 の一般解の導出と 基本例題を解いていく。. 特性方程式の解が 重解となる場合 は除いた。. はじめて微分方程式を解く人でも理解できるように説明する。. 【参考】まるわかり!. 定数係数の非同次 . 3.2. Sympy : Python での代数計算 — Scipy lecture notes. 3.2.1.1. Sympy を計算機として使う ¶. 小田原 も あな 保育園
魔 入り まし た 入間 くん 人気 投票Sympy は3つの数値型を持っています: Real, Rational そして Integer. Rational クラスは分子と分母の2つの Integer の対として有理数を表現します, つまり Rational (1,2) は 1/2 を表し, Rational (5,2) は 5/2 を表します: >>> from sympy import * >>> a . 【高校数学Ⅲ】方程式の実数解と虚数解 | 受験の月. よって, {α+α=- ba,αα=α}²= ca} が成立する. 実数解ならば絶対値が1になるのは x=1 の場合のみなので, 各場合についてaを求めればよい. 虚数解の場合, {虚数解をもつ条件 (D<0)を確認した上で解と係数の関係を利用}する. α=α} なので, α}=1 になるように実数 . ルート2が無理数であることの4通りの証明 | 高校数学の美しい物語. ルート2が無理数であることの4通りの証明. レベル: ★ 入試対策. 式の計算. 更新 2021/03/07. sqrt {2} 2 は無理数である。. より一般に,平方数でない正の整数 n n に対して sqrt {n} n は無理数である。. ルート2が無理数であることを4通りの方法で証明します . 有理数と無理数の意味といろいろな例 | 高校数学の美しい物語. 無理数の例. は無理数です。. 以下のように証明できます。. sqrt {2} 2 が有理数であると仮定する。. このとき,互いに素な正の整数 p,q p,q を用いて sqrt {2}=dfrac {q} {p} 2 = pq とおける。. 左辺は 2 2 の倍数なので q^2 q2 は 2 2 の倍数。. よって q q は 2 2 の倍数 . 方程式の解の問題です。aを三次方程式x^3+3x^2+x+1=0. - Yahoo!知恵袋. 方程式の解の問題です。aを三次方程式x^3+3x^2+x+1=0の実数解とする。このとき、a^3+pa^2+qa+r=0を満たす有理数p,q,rを求めよ。です。記述でしっかりとした解答をつくりたいので教えてください。 答えは、(p,q,r)=(3,1,1)だと思います。 答えは当たり前に感じるけど,ちゃんと証明するには,そこそこ深い . x^3-3x-1=0が有理数の解を持たないことを証明したいのですがなかなかう. - Yahoo!知恵袋. きちんと証明してみます。. 方程式x^3-3x-1=0が有理数解を持つと仮定すると、 その解はa/b(a, bは互いに素な整数で、b>0)と表わされるので (a/b)^3-3 (a/b)-1=0 両辺にb^3をかけてから変形すると a^3= (3ab^2+b^2)b よって、bはa^3の約数です。. そして、aとb . 方程计算器 - Symbolab 数学求解器. 免费的方程计算器 - 一步步求解线性方程,二次方程,多项式方程,根式方程,指数方程,对数方程。输入方程即可获得解,步骤和 . Desmos | Graphing Calculator. Desmos Graphing Calculator Untitled Graph is a powerful and interactive tool for creating and exploring graphs of any function, equation, or inequality. You can customize your graph with colors, labels, sliders, tables, and more. You can also share your graph with others or export it to different formats. Whether you are a student, teacher, or enthusiast, Desmos Graphing Calculator Untitled . 代数方程式の求解 - MATLAB & Simulink - MathWorks 日本. solx は、2 次方程式の 2 つの解をもつシンボリック ベクトルです。 入力 eqn が式であり、方程式ではない場合、solve は方程式 eqn == 0 を求解します。. x 以外の変数を求めるには、代わりにその変数を指定します。 たとえば、eqn を解いて b を求めるには次のようにします。. 住宅 ローン ブラック でも 通る
髪の毛 束 で 抜けるa.b.cは整数とする.3次方程式x^3+ax^2+bx+c=0が有理数の. - Yahoo!知恵袋. 三次方程式って一般的な解公式がないので、まず適当に代入して1解見つけてから二次方程式にして解くという手順でやっているのですが、最初に特殊解を見つけるのにいつも苦労してしまいます。特殊解をすぐに見つけられ るコツがあれば教えてください。. 数学の「超越数論」を独学するための教科書pdf。「代数的数論」の発展分野で,未解決問題多し - 主に言語とシステム開発に関して. 数学・数論の一分野で,「 超越数論 」を勉強するためのフリーPDFのまとめ。 円周率πや,ネイピア数 e などの「超越数」を研究する分野。 超越数とは,「代数的数(=代数方程式の解)ではない数」のことである。 したがって,代数的数論の延長線上に超越数論がある,と考えてよい。. 単振動の運動方程式と一般解 | 高校物理の備忘録. 単振動の運動方程式と一般解. ばねの伸び縮みや振れ角が微小な振り子運動のような, 周期性を持つ振動現象の中で最も基本的かつ重要な問題として 単振動 について考えることにしよう. まずは 単振動をする物体がどんな運動方程式で記述されるのか を紹介 . ド・モアブルの定理 - Wikipedia. ド・モアブルの定理(ド・モアブルのていり、英: de Moivres theorem; ド・モアブルの公式(ド・モアブルのこうしき)ともいう)とは、複素数(特に実数) θ および整数 n に対して (+) = +が成り立つという、複素数と三角関数に関する定理である。 定理の名称はアブラーム・ド・モアブル (Abraham de . 解と係数の関係. 2x 2 +5x+1=0 の解と係数の関係から. α+β =− 52n , αβ = 12n これにより,求める方程式の2つの解 2 α ,2 β については 2 α +2 β =−5 , 2 α ·2 β =2 が成り立つから 求める方程式は x 2 +5x+2=0 …(答). ※ 与えられた方程式についての「解と係数の関係」から,求める . 方程式を解く方法—Wolfram言語ドキュメント. 方程式に一次関数あるいは多項式のみが含まれている場合には, NSolve を使ってすべての解に対する近似数値を得ることができる.しかし,方程式にもっと複雑な関数が含まれる場合には,一般にすべての解を数値的にでも求めるような系統だった方法は . x=√3-1分の√3+1が2次方程式x^2+px+q=0の解となる. - Yahoo!知恵袋. ある整数の2乗の形で表すことができる整数を平方数と呼ぶこととする。5つの連続する奇数の3乗の和で表される自然数のうち、平方数でもあるような数で最小の数は何か。次の中から1つ選べ。【a】225【b】625【c】1225【d】2025. 高次方程式における共役の解同士の関係 - 有理数係数(実数係数?)の高次方程式. - Yahoo!知恵袋. 高次方程式における共役の解同士の関係 有理数係数(実数係数?)の高次方程式において、iを虚数単位としてp+qiが解のひとつであるなら、その共役、p-qiも解であることを示すという有名問題を授業でやったにもかかわらず、忘. 自由研究:有理数に収束する級数を探せ!(超幾何級数の面白い応用) - tsujimotterのノートブック. 変数の数が多いので、おどろおどろしい姿にみえますね。超幾何級数はガウスによって研究されていたことで知られています。たとえば、五次方程式の超越的な解を求めるためにも使われていたりするそうです。. Microsoft Math Solver - 数式問題解法&計算機. スペイン語、ヒンディー語、ドイツ語などでも利用できます. オンライン数学解決アプリは、無料で段階的に代数や微積分等様々な数学の問題を解明します。. 詳細はウェブまたは数学解決アプリでご確認ください。. 二次方程式の意味と解き方まとめ【解の公式・因数分解】|アタリマエ!. 二次方程式の意味と解き方まとめ【解の公式・因数分解】. 二次方程式とは、2x 2 +3x+1=3 のような「xの2乗までを含む方程式」のことを言います。. 二次方程式の意味をキチンと理解するために、「方程式」と「2乗する」の意味から確認していきましょう . 三次方程式の解 - 高精度計算サイト. 
使用目的 答えの確認 ご意見・ご感想 皆さんにも解いてほしいのですが、x^3-6x^2+12x-15=0の実数解を求めよ、で実際は実数解(無理数)1つに虚数解2つでグラフがかければ気づける問題なのですが、最初は全く分からずここを使わせていただきました。. 【整数の性質が超わかる!】 1次不定方程式の整数解の見つけ方 (高校数学Ⅰ・A) - YouTube. 【整数の性質が面白いぐらいわかるようになる!YouTube動画リスト】ww.youtube.com/playlist?list=PLd3yb0oVJ_W16tpeV2Y4Vz1D96OVctza6 . PDF 方程式的公式解(根式解). 但並不是所有的五次或五次以上方程式均無根式解,因此問題又轉移到了 怎樣的方程式才有根式解。這問題沒有困擾人們多久。在1831年,法國數學家伽 羅瓦(Galois,1811—1832)就提出了方程式有根式解的充分必要條件(*)。至此,方 程式的根式解問題也就此劃下 . x^3+2x^2+2=0は有理数の解をもたないことを背理法を用. - Yahoo!知恵袋. ベストアンサー. x^3+2x^2+2=0は有理数の解x=n/m (m,nは互いに素)をもつとする。. 代入して (n/m)^3+2 (n/m)^2+2=0 整理するとn^3=-2m (m^2+n^2) したがって、n^3は偶数 よって、nは偶数 n=2pとおくと、8p^3=-2m (m^2+4p^2) 整理して、m^3=-4p^2m-4p^3=-4p (pm+p^2) m^3は偶数であるからmも偶数 m . カルダノの公式と例題【三次方程式の解の公式】 | 高校数学の美しい物語. 高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください!. すべての有理数係数の2次方程式は2の3乗根を解にもたないこと. - Yahoo!知恵袋. 自分の選択肢を保持する場合→正解率は3分の1司会者が残り2つのうちハズレを消した後に残りに掛ける場合→3つのうちの2つを選んだことになるので当然お得で、これが正解だったので、なんで間違えんねん?. 趣味の数学問題集 A問題 - izumi-math.jp. はじめに. 自分 の 嫌 な ところ
ワーキング ホリデー やめた 方 が いいこの問題集は私が高校時代に作成した問題(100題程度)と大学時代に作成した問題,教員になり作成・編集した問題をまとめたものである.. 高校時代の私の趣味は,自分で作った問題を先生方に解いてもらうことであった.問題の中には先生方で . 43X+32y=4の整数解 - Wolfram|Alpha. 43X+32y=4の整数解. 自然言語. 数学入力. 拡張キーボード. 
アップロード. ランダムな例を使う. 何百万人もの学生やプロフェッショナルに信頼されているWolframの画期的なテクノロジーと知識ベースを使って答を計算します.数学,科学,栄養学,歴史,地理 . 一元二次方程式 - 維基百科,自由的百科全書. 在方程式的兩邊同時乘以二次項未知數的係數的四倍;在方程式的兩邊同時加上一次項未知數的係數的平方;然後在方程式的兩邊同時開二次方根。 將其轉化為數學語言:解關於 x {displaystyle x} 的方程式 a x 2 + b x = − c {displaystyle ax^{2}+bx=-c}. xに関する方程式4x^3-(a-2)x-a-4=0が整数でない正の有理. - Yahoo!知恵袋. 求める解を x = m/n とおいてみましょう♪ ただし m, n は正の数で互いに素であり n ≧ 2 です☆ これを方程式に代入すると 4m³/n³ - (a - 2)m/n - a - 4 = 0 より 4m³/n² = (a - 2)m + (a + 4)n であり この右辺は整数なので左辺も整数になる必要があり m, n が互いに素であるため 4/n² が整数であることから n ≧ 2 . 次の問題の解き方を教えてください!!方程式x^3+px+q=0. - Yahoo!知恵袋. 次の問題の解き方を教えてください!!方程式x^3+px+q=0の1つの解が√3-1であるとき、整数p,qの値を求めよ。また、ほかの2つの解を求めよ。 x^3+px+q=0の1つの解が√3-1であるから. 分数の指数(有理数の指数). 分数(有理数)の指数が付いている式は累乗根で表される式と同じものです.多くの場合,分数の指数を使って計算する方が累乗根のまま計算するよりも簡単になります.. 分数(有理数)の指数の定義. a>0 であって m, n が正の整数であるとき. a. mnn =. n√ . 3次方程式まとめ(解き方・因数分解・解と係数の関係) | 理系ラボ. 東大塾長の山田です。 このページでは、「3次方程式の解き方」と「3次方程式の解と係数の関係」についてまとめています。 ぜひ勉強の参考にしてください!(この記事は、以下の記事の内容をまとめたものです) 1. 3次方程式の解き方まとめ まずは「. 高次方程式のまとめ(解き方・因数分解) - 理系ラボ. 数学Ⅱ2019.05.29. 高次方程式のまとめ(解き方・因数分解). 東大塾長の山田です。. このページでは、「高次方程式の解き方」について、例題を解きながらパターンに分けて解説します。. また、高次方程式を解くときに重要な「因数定理」に関しての . ナビエ-ストークス方程式の解の存在と滑らかさ - Wikipedia. この問題を解の存在と滑らかさの問題という。. ナビエ-ストークス方程式の理解が、乱流のとらえどころのない現象の理解という第一段階と考えられているので、 Clay Mathematics Institute ( クレイ数学研究所 )は2000年5月にこの問題を、数学の 7つの . 5次方程式の解. 上の有名な定理は,実際に数値で係数が与えられたときに「5次方程式が解けない」ことを意味しているのではない.例えば,次の5次方程式は解ける. x 5 −5x 4 +8x 3 +32x 2 −153x+117=0 …. (2) 例えば,初めは適当な値(右図では−0.5の値)から接線を引いてx軸と . 【高校数学】 数Ⅱ-28 2次方程式の解と判別式① - YouTube. 前回 【oo.gl/DHSW0E】 次回 【oo.gl/dFsbPn】ホームページ(19ch) 【ww.19ch.tv/】サブチャンネル 【とある男が . 中学数学2年 連立方程式 - Wikibooks. このように、二つ以上の方程式を組にしたものを 連立方程式 れんりつほうていしき という。. また、その連立方程式に代入することですべての方程式が成立する文字の値の組を 連立方程式の解 といい、その解を求めることを 連立方程式を解く という . Python, SymPyの使い方(因数分解、方程式、微分積分など). SymPyは代数計算(数式処理)を行うPythonのライブラリ。. 因数分解したり、方程式(連立方程式)を解いたり、微分積分を計算したりすることができる。. 公式サイト: SymPy. ここでは、SymPyの基本的な使い方として、. インストール. 変数、式を定義: sympy.symbol . aは整数とする。2次方程式x^2+3x+a=0が有理数の解をもつならば、. - Yahoo!知恵袋. たまたまaの値が偶数の-4のときこの方程式が有理数解を持つからといって、それは証明にはなりません。他のすべての奇数のaについて、有理数解がないということが証明できていないからです。 証明は次のように行います。 解をα、βとします。. Solvers - SymPy 1.12 documentation. The first argument for solve () is an equation (equaled to zero) and the second argument is the symbol that we want to solve the equation for. sympy.solvers.solvers.solve(f, *symbols, **flags) [source] #. Algebraically solves equations and systems of equations. Parameters:. 中2_二元一次方程式_解の求め方(日本語版) - YouTube. 京都教育大学公式YouTubeでは、小・中学校の各教科の学習をサポートするデジタルコンテンツを提供します。3分程度で教科の内容のポイントが . 二次方程式の解 - 高精度計算サイト. この方程式の計算結果があっているかを確認するために使用しました。 バグの報告 a = 1, b = 140, c = -576 の時、 x = -144, 4 と表示されます。 x^2 + 140x - 576 = 0 なので、 x = 144, -4 のような気がしますが. 方程式の解き方 - 中学校数学・学習サイト. 方程式. 方程式とは = (イコール、等号)を用いて数量の関係を表した式が等式である。 式の中にある値を代入すると成り立つ等式を 方程式 という。 また、方程式を成り立たせる値を 解 といい、方程式の解をもとめることを 「方程式を解く」 という。 【例】 方程式 3x - 1 = x + 5について. 高1数学の問題で質問です。xに関する方程式mx^2+5(m+1. - Yahoo!知恵袋. 高1数学の問題で質問です。xに関する方程式mx^2+5(m+1)+4(m+2)=0が有理数の解を持つとき、整数mの値を求めよという問題です。どうやって有理数にしぼるのかわかりません判別式 とかは使うのでしょうか?教えてくださいm(__)m romerofr123456さんmx^2+5(m+1)x+4(m+2)=0・・・①ですよね。[1]m=0のとき①は5x+8=0 カフス を つける 男性